Invention for Encryption & decryption techniques using the shuffle function

Invented by Paul Ying-Fung Wu, Richard J. Nathan, Harry Leslie Tredennick, Jonetix Corp

The Jonetix Corp invention works as follows

Encryption or decryption techniques that are based on one or several transposition vectors. The secret key is used for generating vectors that describe permutation or repositioning of characters within segments of length equal to the length of the transposition vector. The encryption process then inherits the transposition vector and shifts characters. In one embodiment, one or more auxiliary keys, transmitted as clear text header values, are used as initial values to vary the transposition vectors generated from the secret key, e.g., from encryption-to-encryption. Each round of encryption can have associated headers that allow you to?detokenize’. encryption data, and perform rounds of decryption in order to recover the original data or parent token information. FPE (format preserving encryption) is also available with the application to, for example, payment processing.

Background for Encryption & decryption techniques using the shuffle function

The regular practice of keeping proprietary or confidential information in digital devices’ memory and then sending it over unsecure channels has caused significant security concerns. Although the information can be password protected and encryption techniques can be used to make it unusable for hackers or thieves, these techniques can be time-consuming and computationally expensive. They can also require users to memorize complicated passwords to ensure security is sufficient. Even with a carefully chosen password, it’s becoming easier to crack traditional encryption methods. It is possible to make encryption more complicated, for example, by using long keys (e.g. 256 bits keys or longer), but this increases the computational cost of encryption. Key logging and other attacks are still possible.

There is a need for better methods, devices, and systems that can assist in the protection and access of electronic information.

This disclosure provides encryption and decryption techniques, as well products, systems, and software that embody such techniques. More specifically, this disclosure provides encryption and decryption techniques which are based on the use of a shuffle-vector (or transposition-vector), derived from one or more shared (secret) keys. The ASCII text “have a nice one” is a simple example of character transposition. can be shuffled to the?aayvdechdi?en;? This disclosure also provides methods for calculating transposition vectors that are used to shuffle characters or related data. These transposition vectors can also be obtained from secret keys, and optionally from randomizing information. This makes each encryption (from one common secret key or a set of secret keys), different. These techniques can be used at any level of detail within a data set, such as to shuffle bytes. They can also be derived from secret keys and optionally randomizing information that makes each encryption (from a common secret key or set of secrets keys) different. One embodiment shuffles bits in a string that is encrypted or decrypted independently of byte boundaries. Another embodiment derives multiple shuffle vectors (e.g. from respective keys) and shuffles each bit according to a specific vector. The shuffled bits can then be reassembled into bytes, which can then be further shuffled (e.g. on abyte-wise basis). This scheme can be applied to an entire input string or it can be modified from segment-to?segment depending on another transposition vector. These techniques are powerful tools that allow you to permute input strings in a complex way, as should be obvious. These examples, while simple, illustrate the fact that these techniques have many transpositions or variations that will be obvious to those who are skilled in the art.

Thus, the disclosed embodiment provides an encryption method and a decryption technique; an input string is received and, under the control of a digital processing circuitry or processor, it is subjected to the encryption process, which includes the derivation of and the use of at most one transposition vector. The output encryption string is then created. The output encryption string can be stored or transmitted, and it is protected from hackers. Later, the encrypted information can be subject to decryption (including the derivation of and use at least one reciprocal vector as further explained herein) again under the control of a digital processor or circuitry. An output decryption strings is then created. The output decryption string matches that of the input string.

These techniques can be used in another embodiment to create a format-preserving encryption (FPE) technique. There are many systems that require information to fit within certain parameters. These include a numerical-only format or a particular length. Two examples are systems for processing social security numbers and credit card numbers. The techniques described below can be used to encrypt information so that the encrypted information is the same as the original information. For example, the encrypted information can be a 16-digit (base-10) number. One or more shared transposition keys can be used to decrypt the encrypted information. These keys and the associated use character shuffling allow the original number to be derived using the encrypted data. A?character is used in this document. A?character” can be used to refer to any type of information. It could be an individual bit or a collection contiguous bits (e.g. a bit) or a collection noncontiguous bits. There are many possibilities.

Still another specific embodiment presented below applies these techniques to specific applications and systems; for example, another specifically contemplated-implementation provides for a password manager, embodied as a software application on a digital device, where that software application manages numerous identities including credit card numbers, account passwords, identity/social security numbers, and other information (whether such requires a preserved format for communication or encryption or not).

Numerous additional variations and applications are possible for those who have the ability to use the innovative techniques described here.

Remember that the innovative techniques below can be used to add security to your data by permuting the order in which the characters are placed in strings. Below are several techniques that will be described in detail. As an introduction, we will show you how to use encryption in a basic way.

A first user wants to store information that can be retrieved later and protected against hacking or interception. A secret key is generated by the first user. It can be long, complex, arbitrary and random. This key is called a primary key. It can be used in multiple encryption processes. The primary key cannot be shared. It can only be used in data encryption applications (e.g. on the user’s device) and in other applications (e.g. the FPE application described below). However, it can also be used for encryption purposes by the service provider, credit card company or government agency. The first user receives or generates an auxiliary key that serves to randomize application of the primary keys. For example, it can be a time stamp or monotonically increasing number. Combining the auxiliary and primary keys creates a mathematical process which both scrambles the combined data and generates an avalanche effect. This means that even minor differences (e.g. a one-bit difference in auxiliary) can cause large differences in scrambled data (e.g. many bits of combined information are affected by the one-bit difference in auxiliary key). This scrambled information is then subjected to a mathematical process that involves some form of multiplication and finite space math, for example, multiplying each character of the scrambled information and then taking the modulo of that multiplication, character-by-character. The remainders, such as byte-wise numbers, are then sorted in a chosen sort-order (e.g. numerically increasing); this order is used for the transposition vector or shuffle. It is difficult to predict the transposition vector if one does not have all the keys due to the nature of key(s), bit diffusion processes, mathematical operation, and finite space mathematics. This vector then applies the permutation to an encryption process, which in turn is used to encrypt and/or decrypt input text according it’s sort order. Reflecting on this operation, it is noted that the secret key is used to generate the transposition vector; this key is then not directly used to encrypt/decrypt an input string, but rather, the transposition vector is inherited by the encryption/decryption process, and that encryption/decryption of the input string is based on this transposition vector. This design allows for a variety of security options. For example, the secret key may be stored in a container or secured memory on a portable device such as a cell phone. The auxiliary key and input string can then be applied to generate encryption that optionally changes between operations. It is not necessary that the primary key be used beyond the digital device of the user (e.g. or in a protected container). The auxiliary key can be sent in clear to a recipient, and can then be decrypted selectively by the one possessing the secret key. The encrypted information can also be encrypted again if necessary (e.g. double-encrypted with a different secret key and selected secondary key), and can only be decrypted if an entity has each of the primary keys, each round’s auxiliary keys and the order in which they were applied. It is noted again that this example is provided for introductory purposes and that significantly more elaborate encryption/decryption techniques are provided below. One embodiment is discussed below. It uses the primary key (e.g., and an additional key, in one embodiment a time stamp) as well as a nonlinear substitution table to generate a nonlinear substitution list. This is used to apply one element of the overall encryption/decryption process to each segment to be encrypted/decrypted. Another embodiment converts a nonbinary number space into multiple number spaces and provides different processing. This facilitates fast hardware processing (e.g. using simple shifts and adds, XORs and bit inversions and similar hardware logic operations). We will discuss these embodiments in more detail below.

As we have already noted, speed of operation is a major advantage in many embodiments. That is, encryption/decryption is advantageously implemented by digital hardware logic that performs simple shifts, additions and other hardware operations on an input string, without relying significantly on complex mathematical operations performed primarily in software. This processing provides for encryption/decryption processing that is both fast and reliable. Although many of the examples below are relatively simple, they are meant to be explained. However, the techniques described herein can handle very long keys (e.g., keys with 4,000 bits, 2,000 byte, or more complexity). Thus, the described processes can use significantly longer keys than are used in many conventional encryption processes, in large part because the keys (e.g., the primary key) are not directly used in the encryption/decryption of an input string, but rather are used to create one or more transposition vectors.

Another embodiment uses the same techniques to securely exchange passwords with recipients. However, some embodiments allow for complex password generation in transparent ways to users. One example of this is the password manager that has been specifically considered. The primary key is used to convert a simple password (e.g.?have a good day?). The encryption techniques described above are used with padding optionally. The bit diffusion process, e.g. CRC division or another hashing process applied to a progressive character base, is used to completely scramble these values. One or more transposition vectors are then applied to create a more complex, longer password (a “complex code?”). This complex code is then used by the password manager to generate the password. It can optionally be double-encrypted during communications, etc. The password manager can use the original password to recover the password.

Following the discussion below, “Additional applications, embodiments, as well as further advantages of these different applications and embodiments will be obvious to those skilled in art.

Note: Specifically contemplated implementations may include an apparatus containing instructions stored on nontransitory machine-readable medium. Instructional logic can be written in such a way that the general purpose machines (e.g. processors, computers, or other machines) behave like a special purpose machine. This structure is dependent on the instructions and performs specific actions or produces specific outputs. Optionally, such instructions can be embedded on a digital device including such a machine (e.g. one or more processors); the techniques described herein can also be implemented in the form a software program that can be downloaded to and installed on a smart device, digital pad, computer, or another digital device. Alternatively, they can be sold together (i.e., sold with) such a device. ?Non-transitory machine-readable media? (or ?non-transitory computer-readable media?) Any tangible (i.e. physical) storage medium can be used herein, regardless of how it is stored. This includes, without limitation, random acces memory, hard drive memory, optical memory or floppy disk, solid state drive and fuse-based storage. Server storage, volatile and nonvolatile memories and any other tangible mechanisms that allow instructions to be retrieved later by a machine. Machine-readable media can either be in standalone (e.g., program disks or solid state devices) or embedded as part of larger mechanisms, such as a laptop, portable device or server, network, printer or other set of one or several devices. You can implement the instructions in many formats. For example, you can have metadata that invokes a particular action (e.g. Java code or scripting), or code written in a specific programming languages (e.g. C++ code), or any other form. The instructions can also be executed by different processors or cores depending on the embodiment. Such instructions can also take the form of microcontroller-style instructions, which for example, operate special purpose hardware to perform a very limited series of operations. This disclosure will describe various processes. All of these can be implemented using instructions stored on nontransitory machine-readable media. They can also be used to decrypt, encryption or other similar functions. The instructions can also be executed on one computer, depending on how they are implemented. In other cases, however, they can be stored on non-transitory machine-readable media and executed on a distributed basis using web clients, servers or other application-specific devices. Each function is described in the various FIGS. Each function described in the various FIGS can be implemented either as a part of a combined programme or as a separate module. They can be stored on one media expression (e.g. single floppy disc) or on multiple storage devices. This is true for all encryption data generated according the herein. It can be stored on nontransitory machine-readable media, either for temporary or long-term use on the same machine as the other machines. Data can also be stored on media expressions (e.g. single floppy disk) for easy transfer to another machine.

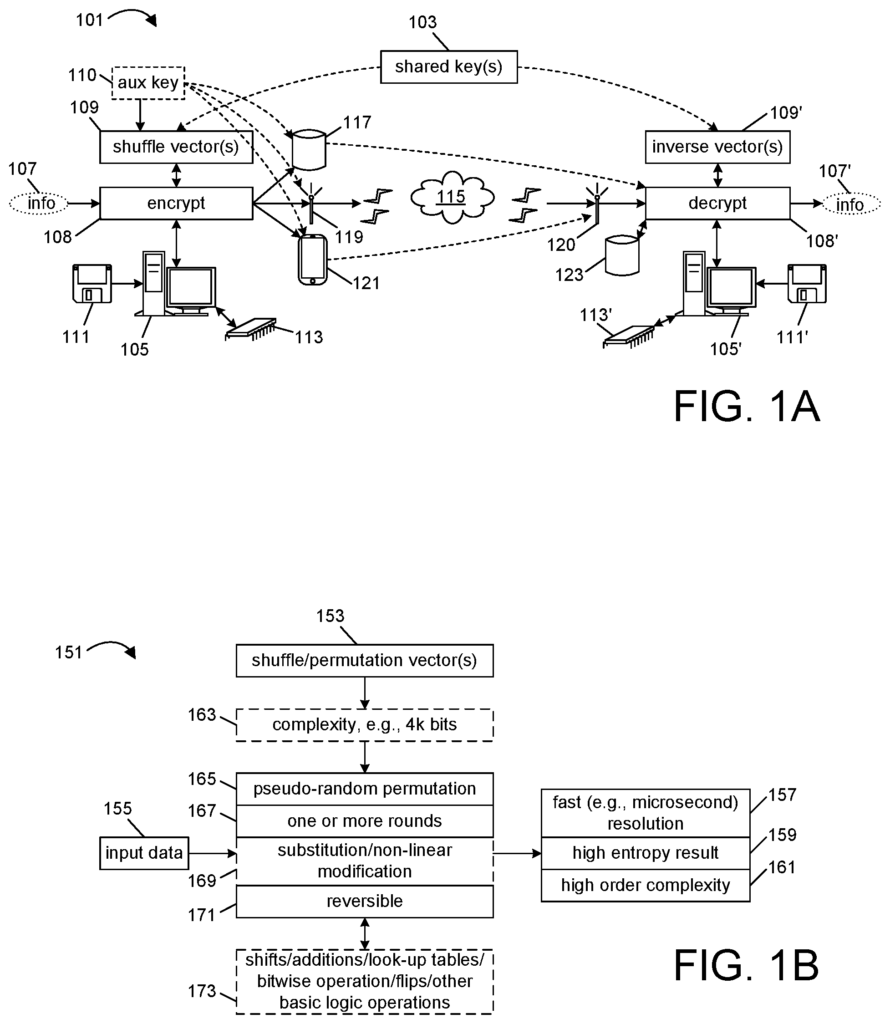
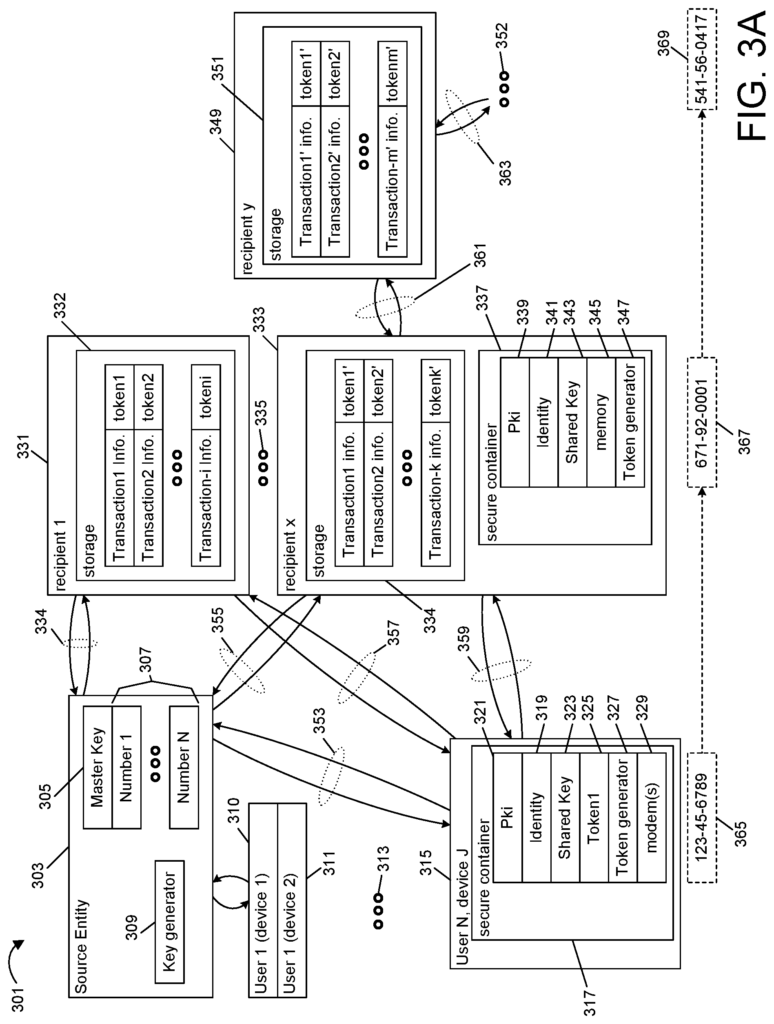
FIG. “FIG. The system is usually referred to using the numeral 101. It is possible to allow a user (108) to encrypt some form of information (107), which will then be stored (117/121) or transmitted (119/121) and later to decrypt (108?). The encrypted information is used to retrieve the original information (107). One user can be the same person (e.g., encrypting the data only on one digital device, 105 or between multiple digital devices owned by the same user), or both can be different users. In this case, the encrypted information will be sent to another digital device (105?). to allow the second user to decrypt it. A shared key 103, as in the previous examples, is used to decrypt and encrypt the information. The first user in many of these examples can be an individual, while the second can be a company or other entity. It is not necessary for all embodiments. The shared key can be generated by credit card companies and given to credit card holders to create tokens. These tokens are format preserving encryptions that are derived from the first credit card number. Clear text transmissions are received by credit card companies (e.g. of transaction information, user identification, etc.) to decrypt a token that was part of a transaction. This information is used to generate or authenticate a credit card number for the individual. If the information matches, and optionally, if any other requirements are met, the card is deemed valid and approved.

The first user will take the information (107) and use the shared key (103) as well as optionally the auxiliary key information 110 to generate one or several transposition vectors (109). The auxiliary key allows the encryption to be different for each process, in effect randomizing how the primary key is applied to generate the shuffling vectors (109). In some cases, a simple time stamp may be used. In a different embodiment that relies upon the use of an auxiliary key 110, the auxiliary key can simply be used as an authentication factor, e.g., the user enters a password, or specifies the location of a file that is used as a secondary key, or software identifies an expected attribute of the digital device 105 (e.g., such as the presence of a specific hardware key, attribute, hash value, which is then interrogated/verified), or in some other manner. The key information, i.e. the shared key103 and/or any additional key 110 is described as providing a transposition key. These vectors describe the reordering bits of input information within a particular length segment to take up different positions within that segment. The first device 105 uses each shuffle vector (109) to encrypt information107 using optional additional processes. The first machine performs or sequences at most some encryption tasks under the control encryption software (denoted with non-transitory media icon 111). It preferably also uses hardware intensive processes that heavily rely on shift and add operations to apply encryption processes to an input string. This hardware intensive process can be conceptually represented by circuitry icons 113. Software 111 is used to control the operations, e.g. to process the primary key or auxiliary key(s), but the hardware intensive process is used to process an input string. It is driven by one of several application-specific circuits that are designed to execute the described processes very quickly (using shifts, additions and other very fast hardware logic operations). It doesn’t matter if application-specific hardware is employed, nor how much software is used to control or perform such operations. The hardware circuit elements acting either alone or under control of such software are referred to as “circuitry.

The encrypted information of one embodiment is stored in machine-readable media or non-transitory storage 117. Thus, the described processes can be used in one application to securely store information for later retrieval (e.g. on the same digital devices 105) or later retrieval and transmission (i.e. either the first user or another user). Another application transmits the encrypted information to a second device (105). The encrypted information is sent to a second digital device (105?) using a modem. 1 by the cloud icon 115. In another application, the information may be displayed visually via a display screen (121), such as a 2-dimensional code or another method of communicating encrypted information. Other methodologies are also possible without departing from the innovative encryption/decryption techniques described herein.

The encrypted information can be received by a second device 105 as described above. to decrypt and/or stored optionally (i.e. in non-transitory medium 123) for later decryption. The second digital device 105 is used in this context. The second digital device 105? is also granted access to the shared keys and can also receive encrypted information (or clear text) from the other key exchangers. However, key exchange technology can also be used to encrypt the auxiliary keys (e.g. PKI). Regardless of key exchange methods, each auxiliary is presumed to have been decrypted at one point and is available in unencrypted format to perform decryption (108?) To recover the original information (107?) The instructions stored on non-transitory machine readable media (111?) can also be included in the second digital device. Circuitry 113? to perform hardware-intensive decryption processes using inverse vectors (109?). The decryption process simply performs the inverted operations of encryption processes, including?unshuffling?. Any permuted characters. To this end, the shared key103 and any additional key110 are used to get the shuffle vectors109 and to compute reverse shuffle information. This includes reordering any shuffled characters back to their original order. Another embodiment does not use reverse shuffling. Instead, the original information (e.g. credit card number) can be encrypted using the shared (secret key) key of the user (retrieved using provided parameters and auxiliary keys to encrypt the original data (e.g. credit card number). Logic is used to detect correspondence (i.e. a match) between the encrypted information and the encrypted information. Both shuffling and unshuffling can be done using hardware-intensive processes. This allows for (optionally) very lengthy strings of input data to use transposition vectors. Further, indirect keys can be used to generate those vectors using very long keys. FIG. FIG.

For example, FIG. 16 refers (153) to the use of one or more shuffling vectors to encrypt and decrypt input data (155). The described processes include transposition or shuffling of characters derived form the input data (and optionally additional processes to take a different format). This allows for extremely fast processing that permits encryption of very long strings of data in microseconds. It also has a high entropy result and high order complexity. This result is very high in entropy as very small changes in input data can create significant differences in encrypted data. It makes it more difficult to use statistical or birthday attacks to crack encryption. Due to the long keys and complexity of the encryption processes, encryption can be extremely complex. The described processes use pseudo-random permutation, which is based on the one (or more) transposition vectors that are derived from any auxiliary keys and the shared key. They can be used in multiple sequential rounds that repeatedly permute, then repermute operands. These rounds can rely on one or several non-linearly substituted or modified processes to further increase complexity. All of this can be reversed to obtain original input data. As indicated by number 173, some or all encryption operations can be performed by hardware logic. This is possible because the keys have been selected and created, and transposition vectors derived from them. It also performs shifts and additions as well as look-up substitutions and other modifications. Bit flipping operations, bitwise processing and other basic logic operations are possible. This is hardware that exchanges operands with other hardware units. As a result of wiring and circuit design, such operations can optionally be orchestrated by software. Software, for instance, can pass operands between multiple circuits (e.g. discrete integrated circuits, or?ICs). Controls the inputs and output of results.

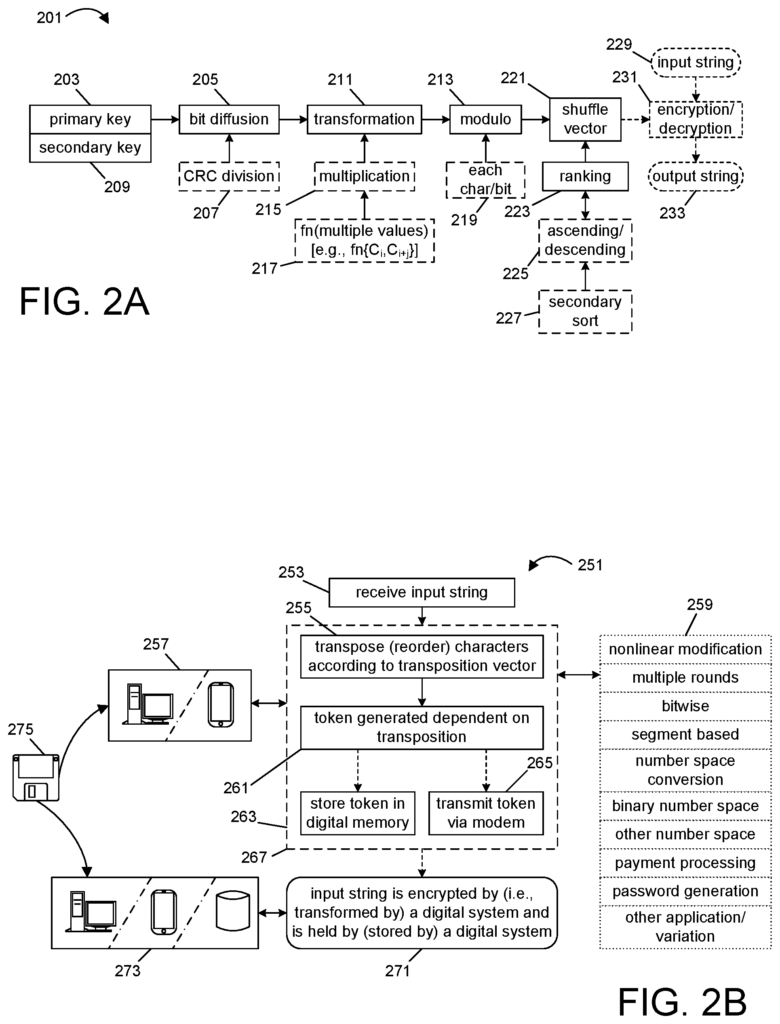
FIG. “FIG. The primary key and optional auxiliary keys are subject to bit diffusion. This uses the avalanche effect to spread small changes in input values to affect many bits, increasing the entropy. The diffusion process can be used to diffuse bits from the auxiliary key(s), or it can be applied directly to the primary key, or both the primary or auxiliary keys. CRC division is one example of such bit diffusion. Any CRC process can easily be used. For example, keys in one embodiment can be converted to binary, combined or concatenated and then divided with a CRC32 polynomial. To illustrate these techniques, an example input string of ?A-Random-Primary-Key!? An example input string of?A-Random-Primary-Key!? and an auxiliary key from?AuxKey8! and a CRC polynomial of x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x+1 will be assumed. The input string and auxiliary key can each be converted to ASCII format, such as 41-2D-52-61-6E-64-6F-6D-2D-50-72-69-6D-61-72-79-2D-4B-65-79-21 (21 bytes), and 41-75-78-48-65-79-21 (8 bytes). The auxiliary key in this example can be prepended to the primary key to form a 28 byte sequence of 41-75-78-4B-65-79-21-41-2D-52-61-6E-64-6F-6D-2D-50-72-69-6D-61-72-79-2D-4B-65-79-21 (28 bytes), which is then converted to binary form, i.e., as a sequence of bits. Dividing the resulting bit sequence by the CRC polynomial (e.g., by 100000100110000010001110110110111) and recording the least significant byte of the quotient at the corresponding least significant byte (LSB) location of the 28 byte sequence creates the value of ?74-F7-A7-E6-44-02-E6-8E-30-F2-69-92-19-53-3F-67-A6-10-C0-9A-13-AB-6E-06-DA-9D-4D-83? The resulting bit sequence is 28 bytes. Only the positions that correspond to the primary key (i.e. the 21 last bytes in the example) are retained. This yields the sequence ?8E-30-F2-69-92-19-53-3F-67-A6-10-C0-9A-13-AB-6E-06-DA-9D-4D-83.? This example uses the auxiliary key as a seed value, or an initial value to randomize the CRC32 division. Optionally, bit wrapping can also be used. For example, the 28 bytes above can be repeated to create a 56-byte sequence. Only the group of least significant bytes (or any other bytes) of the quotient will be extracted for further bit diffusion. There are many variations. You can also use any hashing process to create a sequence of hashed value on a bytewise or other basis, instead of CRC division. This division process effectively applies some form bit diffusion to create a high-entropy result, as previously described, and such bit diffusion is preferably at least applied to diffuse differences in the auxiliary key; for example, if the same input string of ?A-Random-Primary-Key!? If the input string of?A-Random-Primary-Key was used in this example, but with an auxiliary keyboard of?AuxKey9? The output result would be significantly different (i.e. many changed bits of corresponding output relative to the example above) simply because the initial value is slightly different.

Per numeral 211, a transformation process is then applied to the resulting byte array, in this exemplary case, the transformation is applied to the sequence ?8E-30-F2l-69-92-19-53-3F-67-A6-10-C0-9A-13-AB-6E-06-DA-9D-4D-83.? The transformation is usually a per-byte mathematical process that employs functions such as multiplication (215), and operates on multiple bytes (217) to increase complexity. In one embodiment, the mathematical function can be selected to be Result=(Byte(i)*17+IntegerValue*(1+Byte[i+1]), modulo 4096. The value?Integer Value? is used in this example. The randomizing value is obtained by hashing this sequence (e.g. by applying the CRC32 function), to get a value, and then applying finite field mathematics (a modulo a chosen primenumber) to the result. For example, if primenumber 659 is used, the result for the 21-byte sequence is 272. The results of the transformation are then processed on a bytewise basis using finite field math, denoted with the term?modulo. Box 213. This operation generates per-byte (e.g. per-byte) rests which make it difficult to determine the original key values. The transformation function can be chosen in any way you like. However, it is not a fixed function. As indicated in box 219 processing can be applied to other than a byt-wise basis. This means that it can be applied to any combination of one or more bits.

In the case of the sequence, ?8E-30-F2-69-92-19-53-3F-67-A6-10-C0-9A-13-AB-6E-06-DA-9D-4D-83? and the function Result=(Byte[i]*17+272*(1+Byte[i+1]), modulo 4096, the results of transformation, following the application of finite field mathematics, are 3454, 1376, 178, 809, 1362, 2793, 2435, 687, 2119, 3350, 3616, 368, 3962, 2051, 331, 3774, 2326, 1626, 3405, 349 and 163. These values can then be sorted (223) according a soft criteria, usually in ascending numerical order (225). Even with complex transformation functions, it is possible to have?ties? It is difficult to sort these numbers in a unique way. A second function (227), can optionally be used to arbitrate ties. In one embodiment, for example, the original “untransformed” value can be used. In one embodiment, the original?untransformed? values can be used to order?tie. values. Another example is to use a second mathematical function to determine an additional sort index. For example, ASI=(i*83), modulo 249, 69, 152-235, 7:687-69, 8:2119-152, 9:3350-242, 10;3616-60, 11/3762-228, 12/3962-228, 13/3861-55, 12/3962-228, 13/3616-55, 13/3616-228, 13/3862-228, 13:331, 16:349, 17 byte, 18:349, 349, 549, 449, 135549, 19128 111, or other group of bits. The sort index for each position is then paired with the ranking value to produce the following: 0:3454-0; 1:1376-83; 3:809-249; 4:1362-76; 7:687-69. 8:2325-235, 7:3616-62. 13:2051?55. 14:331-138. 15:3774-221. 16:2326-48. 17:1626?131. 18:3405-214. 19:349-41. 20:163456:3456:33666:3456:3456. The array is then sorted by the ranking value. Tie-ups are determined according to the sort indicator. The sorted result identifies the transposition vector. This means that the 21st input (character 20), is to assume first position in a sorted sequence or transposed sequence. The 3rd input (character 2) is then to occupy the 2nd position. The 15th input (character 14), is to assume next position. The shuffle, or transposition vector (221), can then be described as 020.

Click here to view the patent on Google Patents.